概述

在本文中，我们将解释软件JMAG的仿真分析概念。本文中使用的分析模型的数据可以从JMAG应用程序目录下载，因此请使用它来确认设置和结果。此外，建议使用分析模板中现有的几何数据来获得与本文档相同的结果。请以下载分析模型相同的方式下载文件。有关分析模板，请参阅JMAG手册。

本文的主要内容如下：

• 第1节分析目标

• 第2节分析对象

• 第3节分析结果

• 第4节将真实现象转换为分析模型的方法

• 附录A方程式和设定目标

• 附录B优化设置

• 附录C其他设置

• 附录D检查结果

请参阅以下分析内容，来了解分析条件如何设置：

• 磁场分析模型（优化）

• 磁场分析模型（结果）

本文档是使用以下模块和JMAG版本创建的

• 模块DP

• 版本JMAG Designer 19.0

1. 分析目标

一般来说，当气隙的磁通密度接近正弦波时，谐波分量被抑制，效率会有所提高。因此，有一种方法是局部改变SPM磁铁矫顽力，使磁通密度接近正弦波，然而，通过反复尝试，很难找到合适的磁体矫顽力分布。在这种情况下，通过优化，可以有效地得到矫顽力的分布。

在本文中，磁铁被分割成多块，并且定义了矫顽力。先计算出每一块永磁体的矫顽力，通过优化使感应电压波形接近正弦波。将通过优化得到的矫顽力分布与初始方案的电压波形进行了比较。

2. 分析对象

分析目标的前提条件、组成部件、材料、转子磁化强度、绕组、驱动条件、空间磁通密度评估以及本例中处理的优化条件说明如下。

2.1 前提条件

在本例中，分析目标是针对SPM电机（表贴式永磁同步电机）。先决条件如下:

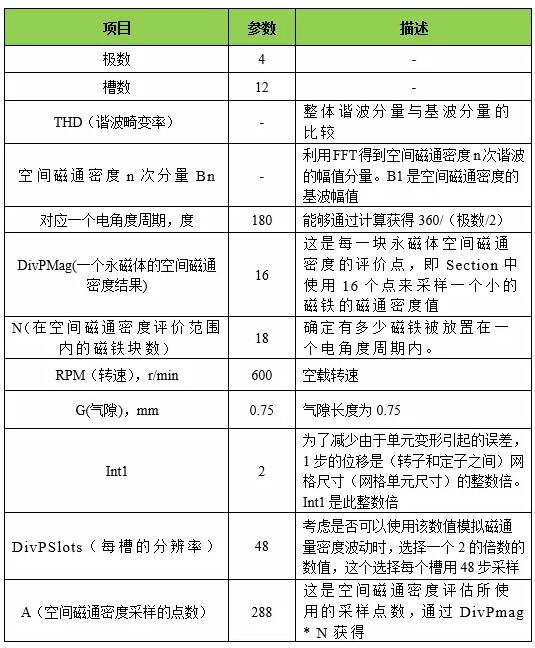
• 组成部件分为内转子和定子。

• 转子是一个由轴以及围绕轴圆周固定位置的块状永磁体组成。

• 定子组件由定子铁心和线圈组成。

• 磁铁为径向磁化，使用不同的矫顽力设计满足要求的电机。

• 进行电机设计时，使感应电压波形更接近正弦波波形。

• 电机叠高大于定子半径。

2.2 组成部分

图2.1显示了分析目标的几何形状和组成部件的名称，表2.1显示了部件规格。

图2.1为分析目标几何形状及组成部件名称，表2.1为部件规格说明。

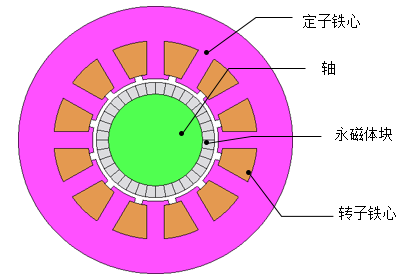
图2.1 分析目标

表2.1 几何尺寸说明

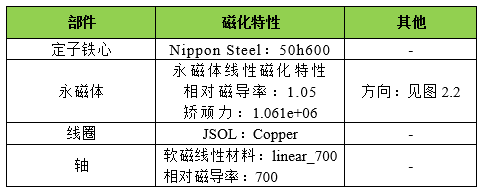
2.3 材料

各个零部件材料见表2.2。

表2.2 零部件材料

2.4 转子磁化

当前的案例的电机极数为4。因此，两极之间的夹角是90度。每一极都将永磁体按每10度来分隔，分成9块，且这些都是为径向磁化。转子磁铁的磁化方向如图2.2所示。

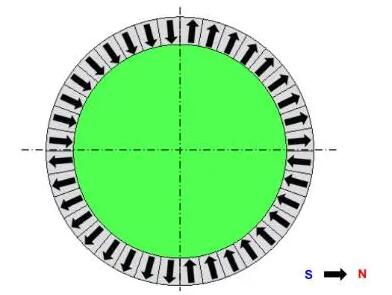
图2.2 转子磁体磁化方向

2.5 线圈

绕组规格见表2.3，分布绕组模型见图2.3。

表2.3 绕线规格

图2.3 分布绕组

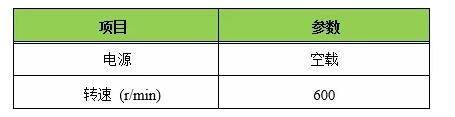
2.6 运动条件

运动条件设置见表2.4所示:

表2.4 运动条件说明

2.7 空间磁通密度评估

图2.4为空间磁通密度评估，得到了转子在空载状态下处于固定位置时的空间磁通密度。

为了使评估结果的正弦性，用总谐波失真(简称THD)来表示信号失真的程度。由于THD是谐波平方和的平方根与基波分量之比，所以THD越小，感应电压波形越接近正弦波。

为每个磁铁块设置不同的矫顽力，并对THD值进行计算。

图2.4 空间磁通密度计算

2.8 优化条件

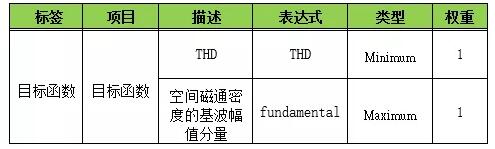
图2.5表明将磁铁作为设计变量，表2.5为设计变量范围，表2.6为目标函数。

设计变量为各个磁铁的矫顽力，其最小值和最大值表示搜索范围。

主要目标是使THD最小，但为了防止由于空间磁通密度太低而无法获得足够的转矩，施加了一个约束以使磁密基波值最大化。

通过满足这些条件，产生的磁通密度达到最大值，波形接近正弦波。

利用上述气隙磁通密度评估公式，设定目标函数，使磁密基波值最大，THD最小。

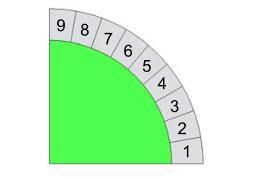
图2.5 永磁体排布（编号1-9）

表2.5 设计变量范围

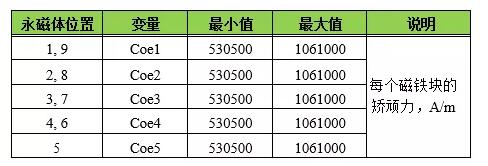
表2.6 目标函数

3. 分析结果

第2节对SPM电机的分析后显示了帕累托曲线、永磁体矫顽力、空间磁通密度波形和感应电压波形。这些结果的确认见附录D。

3.1 帕累托曲线

优化结果的帕累托曲线如图3.1所示。这里采用帕累托曲线上THD最小的设计方案。优化所得到的设计方案在磁通密度空间分布基波分量和THD都比初始案例小。

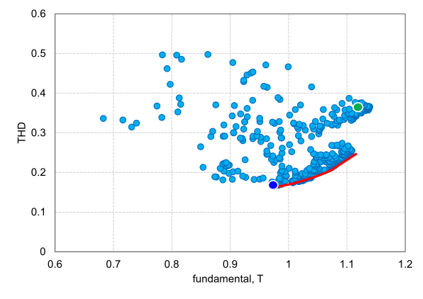
图3.1 帕累托曲线结果

3.2 永磁体块的矫顽力

图3.2显示了通过优化得到的图3.1中蓝点方案的磁铁矫顽力分布情况。从图中可以看出，磁极中心附近的矫顽力增大。

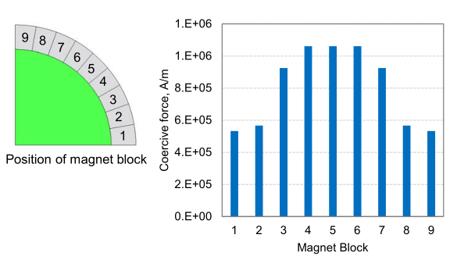
图3.2 局部转子的永磁体的矫顽力分布

3.3 初始案例与优化后的案例的THD

初始案例和优化后案例的THD如表3.1所示。与初始案例相比，优化后的THD值变为原来的约1/2。由此可以看出，优化后的案例比初始案例具有更小的空间谐波与基波的比率，且波形更接近正弦波。

 表3.1 THD值

3.4 空间磁通密度波形

径向空间磁通密度波形如图3.3所示。

波峰和波谷被认为是由磁铁的位置和角度产生的。但通过优化磁体的矫顽力后，可以发现空间磁通密度已经近似成为正弦波的波形。这与上面表3.1的结果一致。

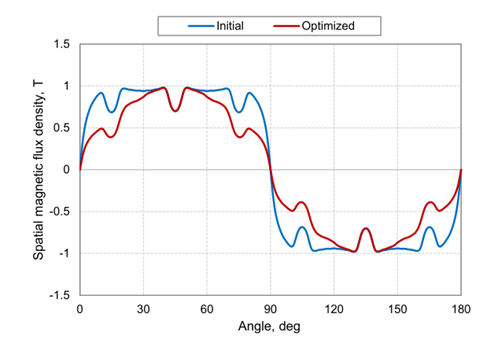
图3.3 空间磁通密度波形

3.5感应电压波形

图3.4为感应电压波形，图3.5为感应电压各频率的幅值分量。

与之前的THD和空间磁通密度波形评估结果相似，通过优化可以确定该波形接近正弦波。

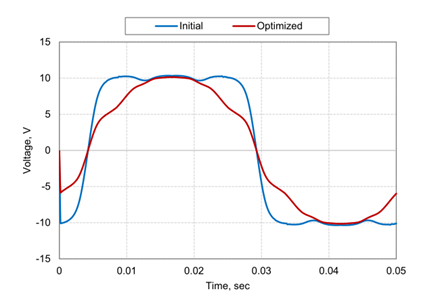
图3.4 感应电压波形

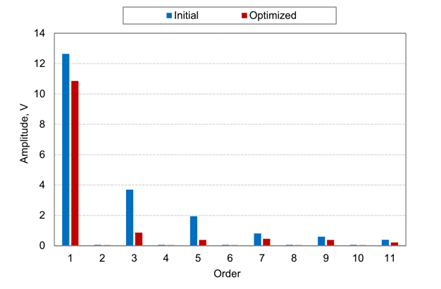
图3.5 感应电压各频率的幅值分量

4. 将真实现象转换为分析模型的方法

4.1用于创建FEM模型的参数

表4.1显示了与设备尺寸参数和仿真计算相关的变量。

表4.1 用于创建FEM模型的参数

4.2 分析模型

在第2节为分析目标创建了一个分析模型。在本例中，执行磁场分析以评估在空载和无旋转情况下气隙中产生的磁通密度。主要的模型参数见表4.2，磁场分析中使用的局部模型如图4.1所示。

图4.1 磁场强度分析的1/4模型

表4-2 用于磁场强度分析的模型参数

4.3 矫顽力优化研究

根据气隙磁通密度分布得到了THD和基波，要寻找具有最小THD和最大基波的磁铁矫顽力。

4.3.1 永磁体矫顽力优化

在本例中，获得了在1个电角周期内在气隙中径向的磁通密度，将得到的磁通量密度用FFT变换得到THD。通过将磁铁的矫顽力作为设计参数变量，得到THD最小且空间磁通密度分布的基波幅值为最大的值。

4.3.2 优化算法

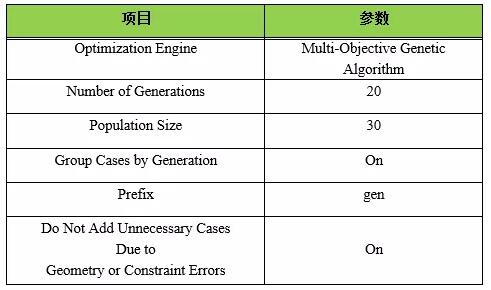
为了获得具有最小的THD值和最大的fundamental值的矫顽力，以这些作为目标函数进行优化。在这个例子中，每个评估项目都存在相互权衡的关系，因此选择一个多目标遗传算法与优化引擎一起使用。

4.3.3 利用多目标遗传算法寻找最优解

为了避免在搜索范围的选择上存在偏差，根据设计参数的数量来确定种群规模。种群规模建议至少为设计参数的数量+1.5倍或更多。建议使用大约10倍，这是因为较大的种群规模大小在搜索空间内的偏差较小，并且可能将对指定的设计空间（搜索空间）进行彻底搜索。

在此数据中，由于设计参数个数为5，所以每一代种群数量为30，即5乘以(5 + 1)所得。

4.3.4 多目标优化算法收敛准则

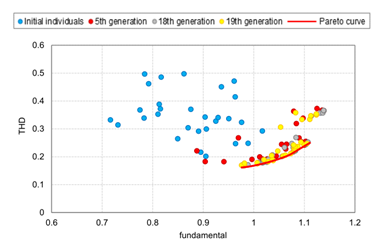
在每一代中使用所获得的评估值来检查是否已获得最佳几何结构（优化是否已收敛）。图4.2显示了每一代获得的特性，几乎所有的第18代和第19代的个体都处于第19代帕累托曲线上。这两代人的性能几乎没有差别，由此可以确定优化在第19代已经收敛。

如果不能确定收敛性，则应增加代数并重新进行优化。如果可以从获得的最后一代中恢复（重新启动）优化，则建议使用此方法。

4.3.5 电路建模

通过对空载磁场强度分析，对磁体产生的磁通密度进行了评估。空载电路如图4.3所示。

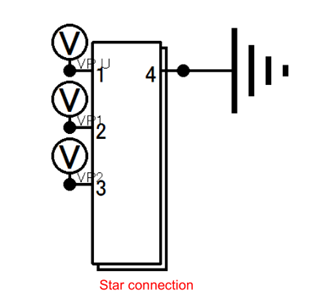
图4.3 空载电路

4.3.6 优化响应值

在优化过程中，由气隙磁通密度分布波形得到THD和基波，并将这些值设定为目标函数作为响应值。在该分析中，为了从空间磁通密度计算得到的THD和基波作为响应值，需要预先设置空气区域的Section截面。另外，利用FFT分析计算磁通密度的空间分布，计算THD和基波，并设定响应值。

<空间磁通密度评估>

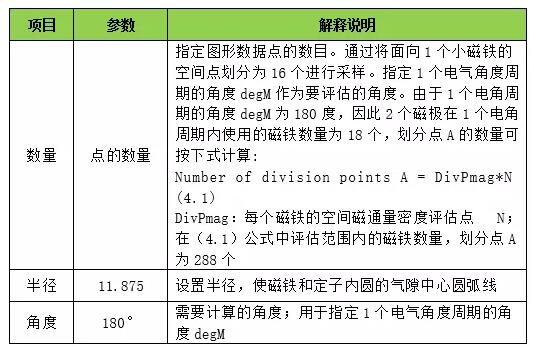
根据获得的气隙空间磁通密度分布，得到响应值。在运行优化之前，必须设置评估空间磁通密度的部分，空气区域的截面圆弧如表4.3所示。

表4.3 截面圆弧与空气域设置

<计算THD值和 fundamental(磁通量密度空间分布基波分量)值>

利用FFT对气隙径向产生的空间磁通密度分布进行分析，对每一频率分量的幅值进行分析，根据（4.2）中的公式得到THD值。

4.3.7 时间离散化

计算得到在1极对气隙中产生的磁通量密度。由于只计算1步，因此没有时间离散化。

4.3.8空间离散化

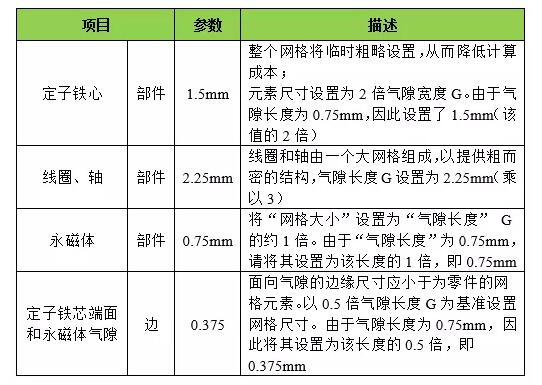
<零件网格大小>

网格尺寸需要根据磁铁和定子之间的气隙设置。为那些能改变磁通量密度的部件（例如气隙等）设置一个准确的网格尺寸，这对于分析结果有着很大的影响。为面向气隙的磁铁设置较小的值。

表4.4 元素大小设置

<圆周方向剖分>

为了准确捕捉气隙内的磁通，必须防止气隙网格变形。如果每一步的位移是气隙网格单元尺寸的整数倍，那么由于单元畸变而引起的误差可以减小（Int1是整数倍）。

在本例中，根据从表4.3中获得的1电周期的评估点A，确定圆周方向上的划分数。

由式（4.1）可知，180度1个电角度的评价点A个数为288个，因此局部模型90度圆周方向上的划分数为A的1/2，即144。

Number of circumferential divisions of partial model Sdiv = A/2* Int1 (4.3)

由于(4.3)中Int1为2，因此局部模型的周向划分数Sdiv为288。

<考虑旋转周期对称性网格>

该模型分析了空载情况下由磁体产生的磁通引起的气隙空间磁通密度。转子位置的时间变化也可以通过使用相同的网格划分，以作为稍后描述的最佳解决方案4.4的分析Study中。为此，还考虑了网格形状旋转的周期性。

4.4最优解分析

为了评估优化结果，对初始case和最佳的case进行了瞬态电磁场响应分析，以便获得感应电压波形。

4.4.1运动条件建模

通过对转子施加恒定旋转条件以改变定子与转子之间的相对位置来进行分析。

4.4.2电路建模

这里的电路建模与4.3.5中相同，这里有必要设置电压探针来评估感应电压。

4.4.3时间离散化

<时间步长>

“划分数”指定每1个电气角度周期的划分数。每步时间增量除以1个电周期时间除以1个电角周期的划分数DivPElec。基于空间磁通密度评估点A，使用以下公式。

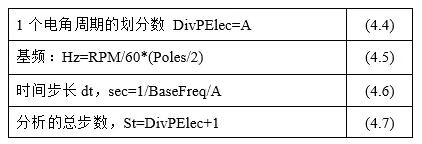
公式（4.6）中的时间步长为1.7361e-4秒，公式（4.7）中的分析步数St为289步。

4.4.4空间离散化

空间离散化设置与4.3.8相同。

附录A 方程式和设定目标

A、1方程式

由方程式定义的变量如表A.1所示:

表A.1 公式列表

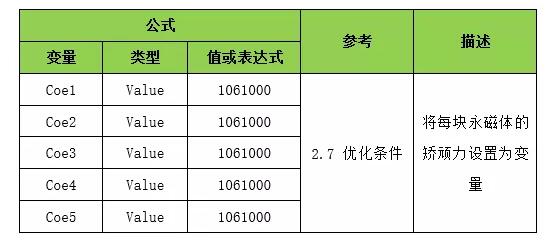
A、2设定目标（磁场分析）

表A.2和图A.1所示为每个磁场分析条件规定的设定目标（组）:

表A.2 设置列表

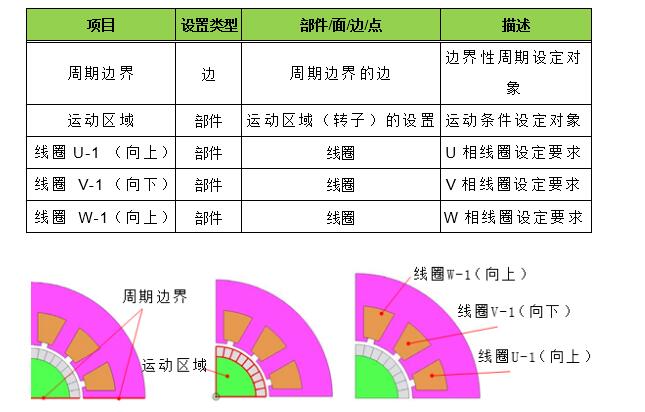
图A.1 磁场分析的条件设置对象

附录B 方程式和设定目标

在本例中，对磁铁矫顽力进行了优化。在优化中，在执行分析之前必须设置一些项目。B.1描述了用于优化的功能，B.2及更高版本描述了在执行优化之前要配置的必要设置。

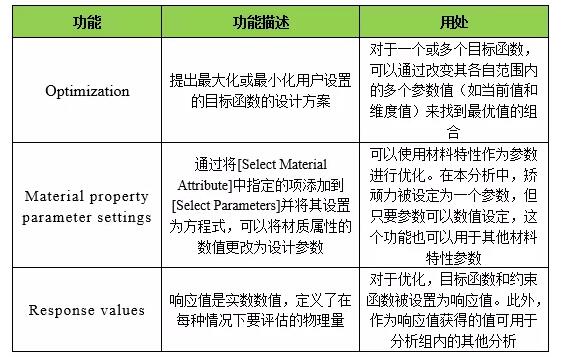
B.1优化中使用的功能

本例中使用的功能如表B.1所示：

表B.1 优化中使用的功能的特性

B.2材料属性参数设置

对于这种材料，采用矫顽力作为设计变量进行优化。

要设置材质特性的参数，请使用自定义材质，从“材质特性”列表中选择要更改的值的参数，然后将该参数设置为材质变量。

有关详细信息，请参见JMAG Designer的帮助文档：Home > Operations > Multiple Calculations > Running Calculations of Multiple Cases with Some Parameters as Variables (Parametric Analysis) > Selecting Parameters Having Values That Will Be Changed (Selecting Design Variables)，然后使用材质特性作为设计变量。

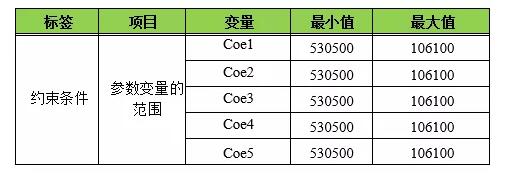
B.2优化设置

具体的优化设置如表B.2至表B.4所示。

表B.2 [Constraint Conditions]选项卡下的优化设定值

表B.3[Objective Functions]标签下的参数设置值 

表B.4 [Options]选项卡下的参数设置值 

附录C 其他设置

C.1 Post-Calculation脚本

准备创建优化响应值的计算后脚本。将通过PostScript得到的THD和 fundamental为响应值。

有关脚本文件的内容，请参阅示例数据的后处理[Post Calculation Scripts]中名称为THD的脚本文件。

附录D 检查结果

第3节分析结果的确认方法如下。

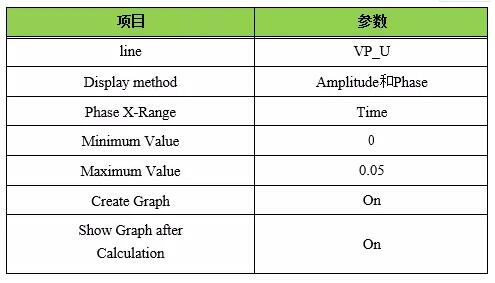
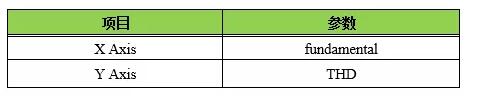
D.1确认与图3.1相同曲线图的优化结果，右键单击[Study:]>[Results]>[Response Graph]下的[Graphs]，选择[Generate]，并设置响应图。表D.1显示了本例中使用的设置。

表D.1显示了本例中使用的设置

D.2 磁铁矫顽力如图3.2所示，右键点击[Study:]>[Results]>[Response Graph]下的[Response Data]，选择[View Response Table]，显示[Response Table]对话框。在图3.1中，在帕累托曲线的最佳方案中，该方案是使用该图中的值来设置每个磁体块的矫顽力值。

D.3初始方案和最佳方案的THD

通过选择[Study:]>[Results]>[Response Graph]>[Response Data]下的[View Response Table]显示[Response Table]对话框，可以显示表3.1中显示的THD值。框，确认初始方案和优化方案的THD值。

D.4空间磁通密度波形

图3.3所示的空间磁通量密度波形通过右键点击[Study:]>[Results]>[Section]下的[Magnetic Flux Density]，然后选择[Show All Cases]。选中图形的[Line Options]选项卡上初始案例和最佳案例旁边的复选框，以显示图形。

D.5感应电压波形

图3.4中显示的感应电压波形通过右键单击[Study:]>[Results]下的[Graphs]来显示，将鼠标指针移动到[Circuit voltage]上并选择[Show All Cases]。

在从图形对话框显示感应电压波形后（图3.4），再显示了感应电压波形FFT，如图3.5所示。从[Calculation]>[Fourier Transform]进行FFT后将数据导出到电子表格软件（如Excel等），并在电子表格软件中显示图3.5。表D.2显示了JMAG-Designer傅里叶变换的设置。

表D.2 在分析组中响应图的设置