在工程设计中,最优解永远是追求的最终目标,但产品因为批量生产导致良率降低、或产品因环境波动而性能不稳时,此时就需要考虑在理论下的最优设计,在实际生产时及其的不稳定。
这就是忽视鲁棒性所带来的代价。那么,究竟什么是鲁棒性呢?它为何可以为设计提供最稳定的设计方案呢?
一、鲁棒性:在不确定性因素中的定海神针
比如两款冰箱:A & B
A冰箱在恒温实验室里是节能冠军,但是在用户家里遇到夏天高温或电压波动时,耗电量飙升甚至出现其他状况;
B冰箱在恒温实验室里数据不如A,但是在用户家中无论严寒酷暑、电压波动,性能始终稳定,故障率比A冰箱低。
而B冰箱的性能,就是产品设计追求的鲁棒性;
鲁棒性,Robustness,指系统或产品存在内部参数波动、外部环境变化、制造工差、使用磨损等不确定因素时,仍能保持其预期功能和性能稳定的能力。它不是实验室或者计算机仿真计算中的最优解或峰值,而是确保实际情况下的可靠交付能力。
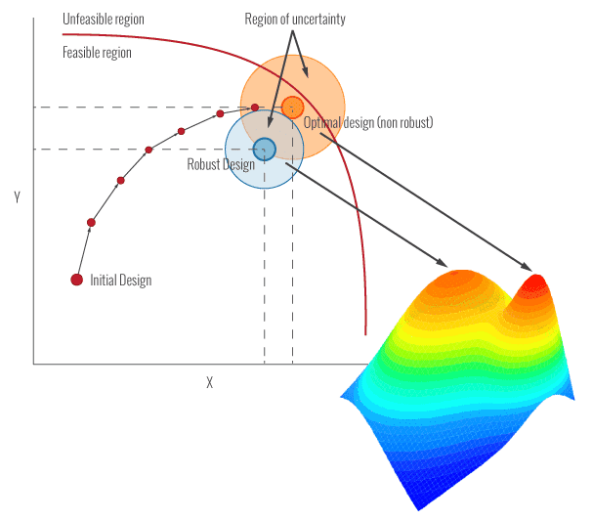
因此鲁棒性强调的是在真实复杂环境中,产品面对各种不确定因素时的适应与稳定能力。例如:
1:制造公差不可避免:材料批次差异、加工精度限制、装配误差;完美的数据只存在于图纸;
2:环境条件复杂多变:温度、湿度、粉尘、干扰等;恒温恒湿数据只存在于实验室;
3:使用负载难以预测:用户操作习惯、长期老化;设计需要包容未知性;
......
一个具备鲁棒性的设计,往往能包容更多变量波动,将性能稳定在可接受范围内,而不是依赖理想条件下精准控制的完美状态。因此,在设计过程中,提升鲁棒性意味着优先考虑实际使用场景的多样性与挑战性,让产品在不确定中依然可靠运作,这正是设计稳健性的核心价值所在。
二、传统优化设计盲区
传统基于JMAG等CAE工具的优化流程往往是:
1:设定目标(如效率最高、扭矩最大、体积最小);
2:调整设计参数(如磁钢尺寸、绕组匝数、槽型几何);
3:在理想的标称条件下运行仿真计算;
4:利用优化算法找到该条件下性能最优的参数组合;
但是这种确定性优化有一定的隐患:
孤峰陷阱:找到的最优解可能位于一个狭窄的尖峰上。若因制造工差造成参数由偏差,性能就会断崖式下跌;
忽略波动影响:未考虑温度变化导致材料属性(如硅钢片导磁率)改变对性能的影响;
风险后置:把鲁棒性问题留到样机测试甚至量产阶段才发现,代价高昂;
三、modeFRONTIER协助
JMAG实现鲁棒性优化设计
modeFRONTIER作为业界优秀的多目标优化平台,与JMAG深度集成,为解决鲁棒性难题提供了系统化的方法论和强大的工具。
modeFRONTIER鲁棒性优化基本流程:
1:确定不定性参数
识别关键波动参数:哪些参数/环境条件存在不确定性;(如绕组电阻率、工作温度、叠片厚度等);
量化不确定性:定义这些变量的统计分布(如正态分布、均匀分布)、范围或标准差;
定义优化解周围撒点数量:了解优化解在不确定性参数变动下的稳定性;
2:定义鲁棒性目标:
在追求传统目标(效率、扭矩、成本)的同时,将鲁棒性指标纳入优化目标或约束;如效率均值最大化等;
3:优化算法驱动
modeFRONTIER拥有多个知名优化算法(如MOAG-Ⅱ多目标遗传算法、SIMPLEX等)
算法能高效探索设计空间,自动寻找哪些在参数和环境扰动下性能仍然稳定且优异的设计方案,及寻找宽广的高原而非陡峭的孤峰;
四、案例展示:
基于JMAG电机鲁棒性优化案例
案例一:田口法协助JMAG进行电机鲁棒性设计寻找最稳定设计方案
(一汽红旗 - 2024艾迪捷用户大会报告)
考虑到制造公差引起的不确定性响应偏移,通过引入稳健指数目标函数,综合评估电机在大批量生产阶段的制造质量和产品一致性因素,有效提高电机峰值转矩和峰值功率,降低电机阶次电磁力和转矩波动,而且性能波动最小,实现多目标、高鲁棒性的电机优化设计。
具体设计流程如下,通过田口正交表生成DOE,将大大减少设计案例数量,并实现鲁棒性设计分析。
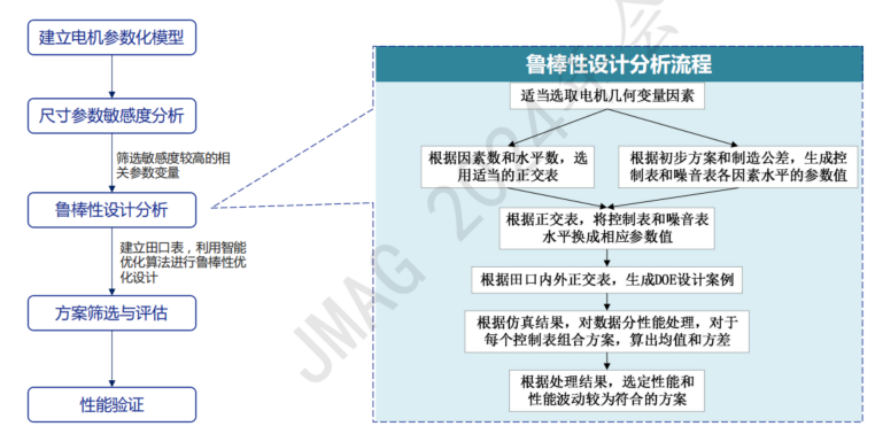
优化流程:
建立电机参数化模型,选取11个关键几何参数作为优化变量
确定初始参数及制造公差,利用代码生成控制表及噪音表,并设置迭代数及样本数
设定优化目标,以54阶电磁力、转矩、转矩波动为优化目标
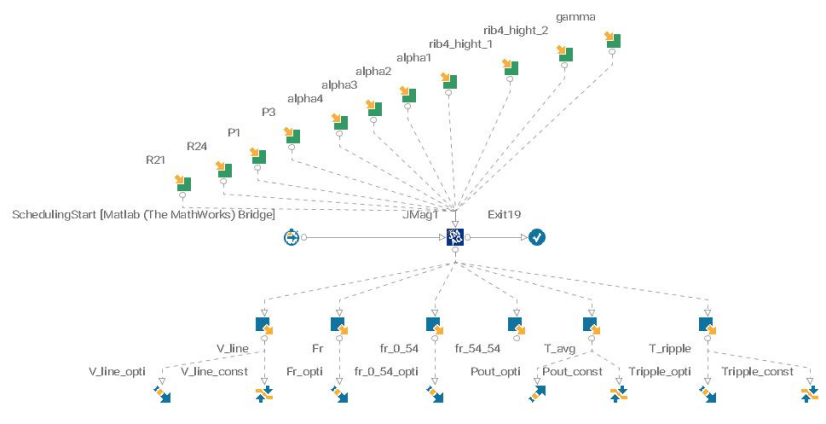
全因子DOE在不考虑噪声影响、三水平的情况下,需要生成177147个case,而田口正交法只需要23个case( L23(3^11) ),降低计算资源占用。
田口正交法包含一个控制表和一个或多个噪音表。表中每个红色数字为该行该列的控制表和噪音表参数叠加后输入到Jmag模型中得到的响应结果;
每个控制变量组合生成了23个结果,对其均值和标准差进行统计分析;
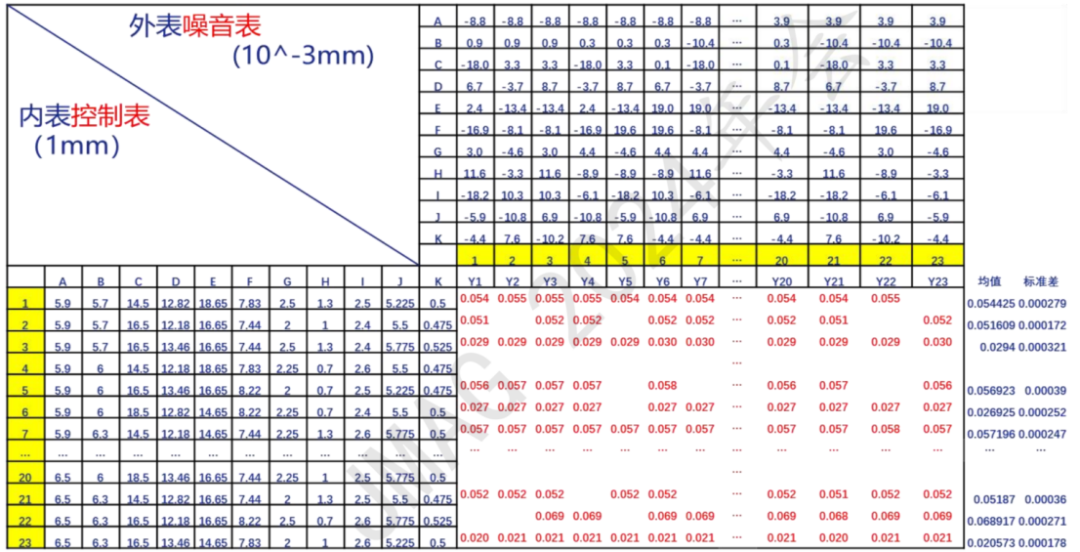
优化结果:
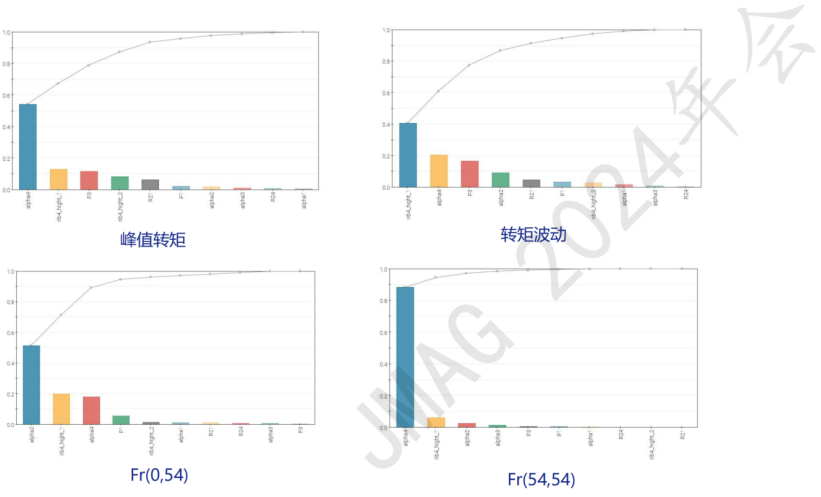
针对电机各尺寸参数进行参数敏感度分析,重点关注(0 54)、(54 54)阶径向力密度、转矩波动
关键参数包括:永磁体宽度、永磁体与Q轴间距离、永磁体槽角度等,在后续优化中可以针对此类参数进行大范围寻优
建立优化目标之间的散点图及平行折线图,确定帕累托前沿曲线,判断优化方案分布区域及优化效果,筛选满足设计需求的优化方案
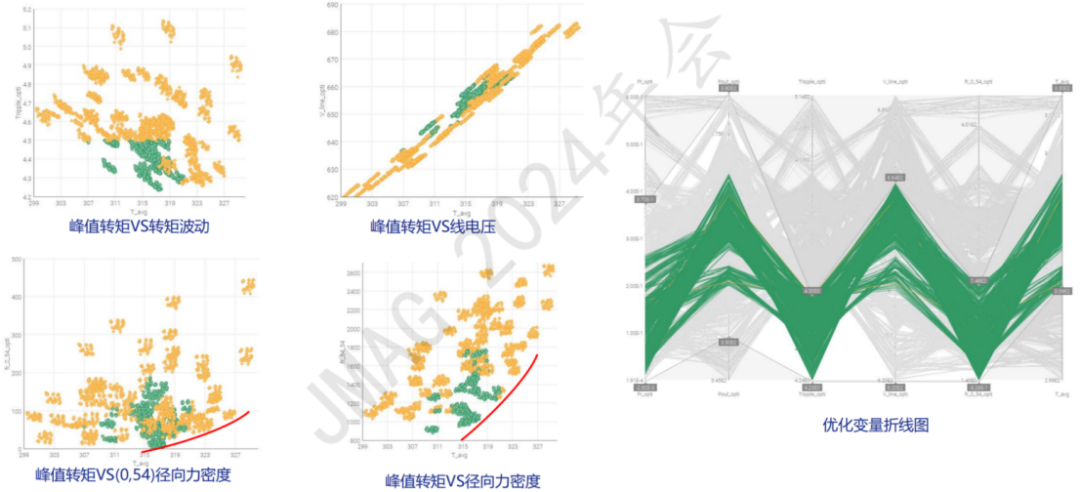
分析优化目标之间的相关性,峰值转矩与转矩波动呈负相关性;(0,54)阶径向力密度、(54,54)阶径向力密度与转矩波动呈正相关性;

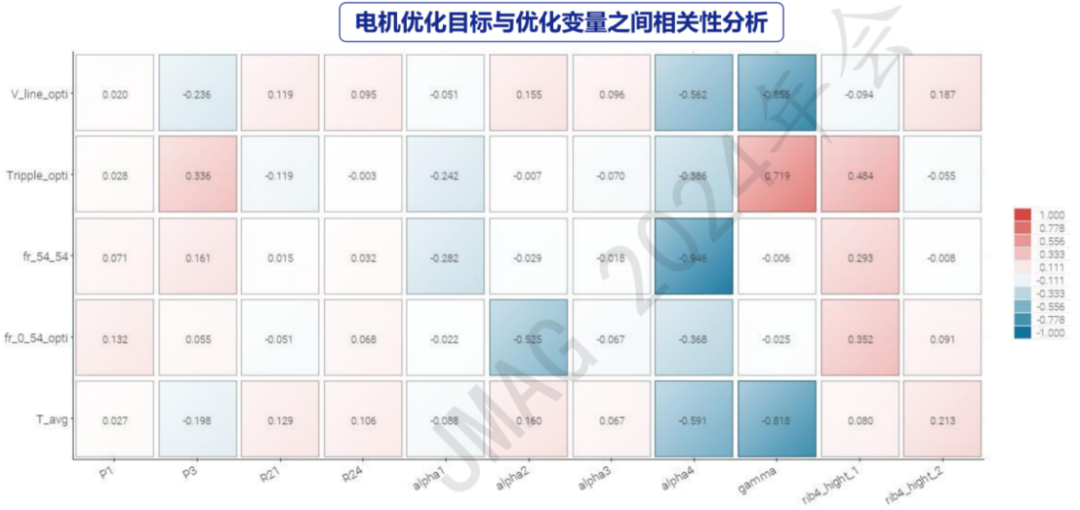
分析优化目标与优化变量之间的相关性,Fr(0,54)与永磁体槽角度呈负相关性;转矩波动与永磁体宽度呈正相关性,与永磁体槽角度呈负相关性
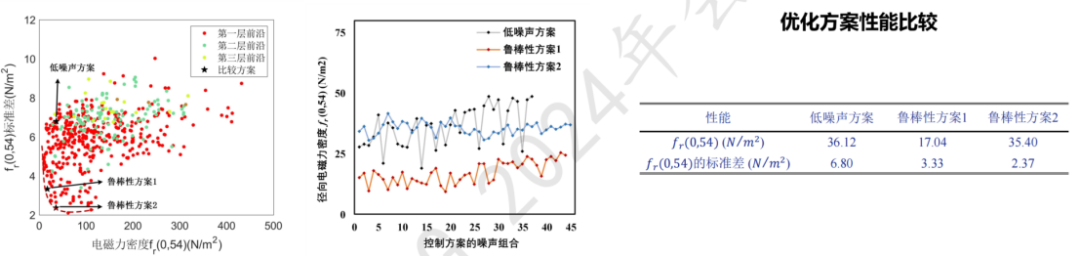
以Fr(0,54)标准差作为鲁棒性评价指标,选取Fr(0,54)和Fr(0,54)标准差较小方案作为鲁棒性优化方案
鲁棒性方案1和鲁棒性方案2的标准差有效降低,鲁棒性均有提高
总结:
1:制造公差对电机核心性能影响较大,为保证批量后性能波动小,需要进行电机鲁棒性设计;
2:基于田口正交表的离散化有限元方法可保证电机鲁棒性分析的精准度,但时间和计算成本较高,可尝试基于代理模型的方法;
3:电机鲁棒性设计做得好,电机的成本才能回归合理水平;
4:电机鲁棒性优化设计是一项重要的工作,是开发高品质电机的基础;
案例二:modeFRONTIER鲁棒性优化设计完成JMAG对PM电机的形状优化
(艾迪捷公司自研案例)
PM电机的形状优化方面需要小型化、低成本、低损失化等各项需求,同时还要满足强度应力、磁钢的不可逆退磁、热、NVH等条件,而这种多条件约束问题,就需要进行多目标优化,并找到最稳定的设计方案。
因此定义7个转、定子形状参数,目标是为了让转矩最大、转矩脉动最小、磁钢体积(面积)最小化。
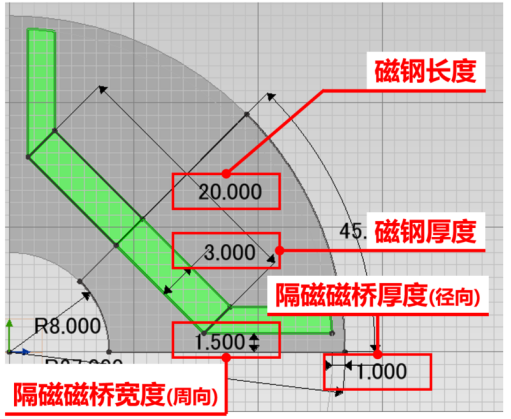
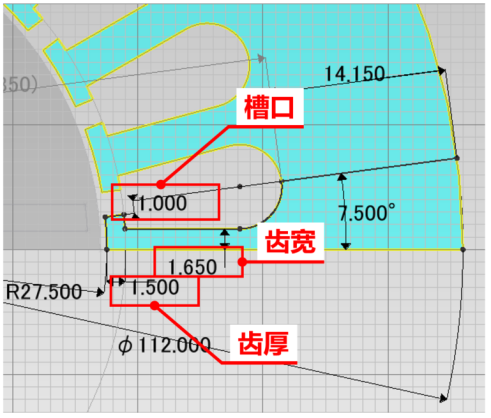
根据以上条件和目标,modeFRONTIER创建优化流程,为了获取较为稳定的设计方案,并非理论意义上的最优解,因此在流程中加入鲁棒性设计优化过程,即在每个设计方案周围进行撒点,通过一定数量上的撒点进行仿真出来的数据进行极值、标准差计算,并把标准差、极值等作为流程的优化目标,以此可以判断出哪种设计方案鲁棒性较好。这也是鲁棒性设计优化的最基础的思路。
而本次优化过程中,计划优化100次,鲁棒性撒点10个,即需要仿真1000次。
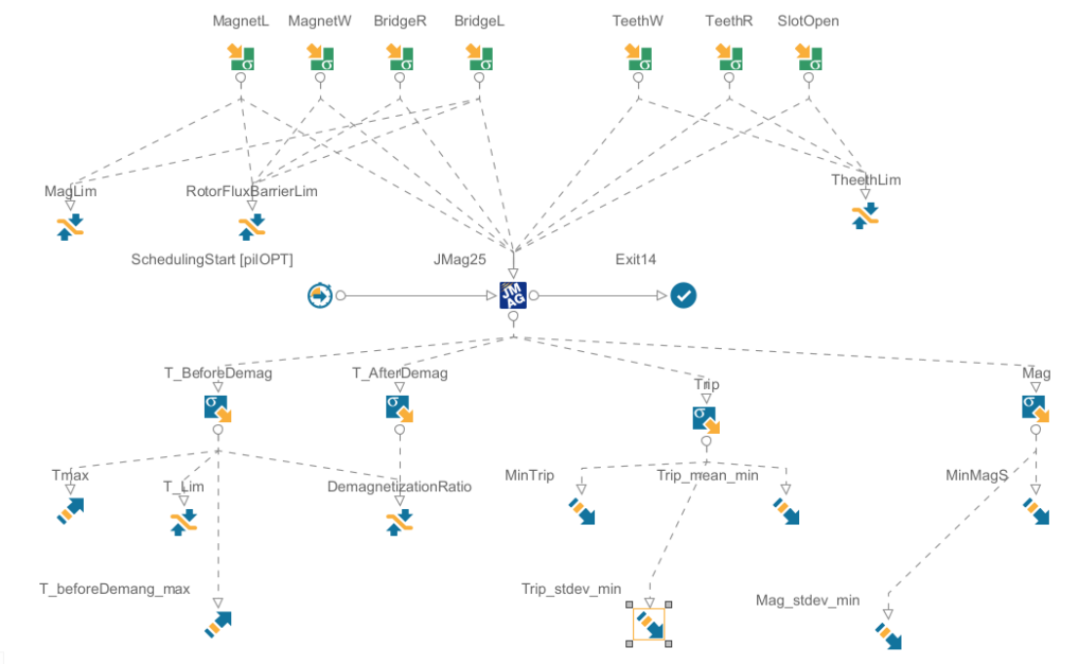
本次优化仿真共耗时9小时29分钟58秒。
优化结果:
全部仿真结果难以查看最稳定设计方案,因此对于鲁棒性优化的100次优化结果进行帕累托筛选,共计筛选出39种设计方案(下右图);
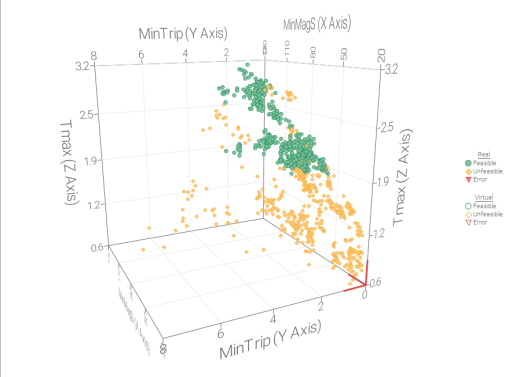
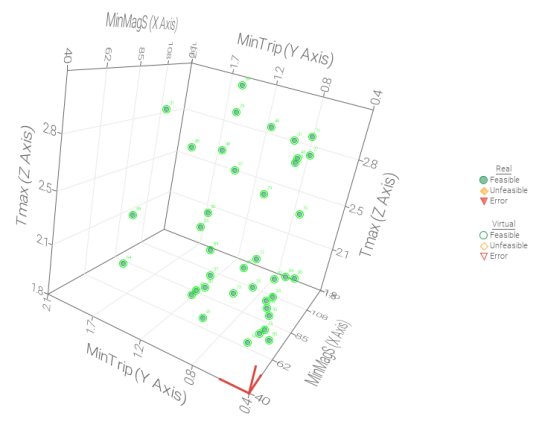
根据帕累托解集,利用平行折线图,可寻找Trip和Mag下的标准差最小,满足标准差小于预设数据情况下筛选出的稳定解。
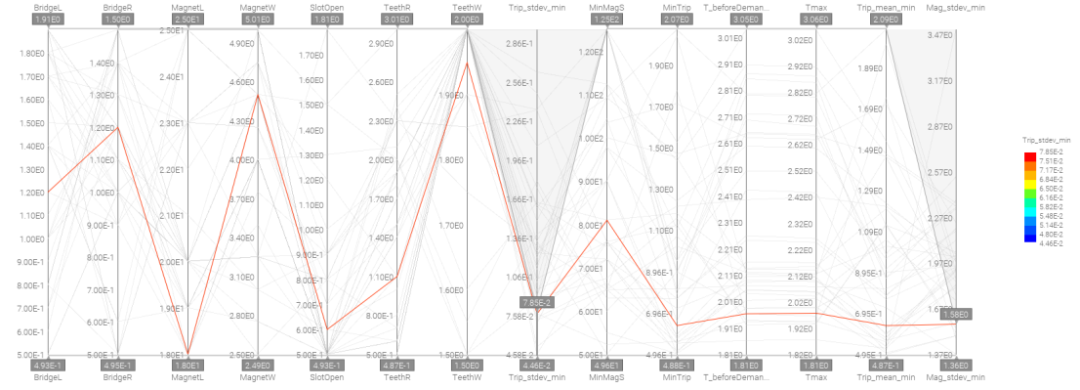
此设计方案仅用作展示作用,即利用目标结果的标准差筛选出最稳定设计方案的整体思路。
此案例利用modeFRONTIER的鲁棒性优化设计功能,在调用JMAG进行电机设计仿真的背景下可以优化出较为稳定或最为稳定的设计方案。
五、协同价值:modeFRONTIER+JMAG
鲁棒性优化是核心,但modeFRONTIER+JMAG结合的价值远不止于此:
1:多物理场协同优化:电机设计涉及电磁、热、结构应力、振动噪声。modeFRONTIER可同时驱动JMAG、结构分析软件、声学软件等,实现真正的多学科优化,寻找电磁性能、热管理、机械强度、NVH性能的全局最优平衡点;
2:大规模参数探索与设计空间导航:面对海量设计参数组合,modeFRONTIER的优化算法能高探索整个设计空间,揭示设计变量与性能间的深层规律,避免工程师陷入局部经验陷阱;
3:响应面模型加速:对于及其耗费时间的仿真分析,modeFRONTIER可基于有限次的精确仿真,构建高精度代理模型,,后续优化可在代理模型上秒级完成,大幅度提升优化效率;
4:流程自动化:将整个设计-仿真-优化流程在modeFRONTIER中固化、自动化运行,避免重复劳动,实现复用;
总结:
当最优的定义从实验室的峰值数据,转变为量产产品在万千用户手中稳定可靠的表现时,鲁棒性优化就不再是技术选项,而是工程智慧的必然选择。modeFRONTIER和JMAG的黄金组合,正是帮助我们在充满不确定性的环境中,确定我们最可靠的设计方案。

 B站账号
B站账号

 知乎账号
知乎账号

 微信账号
微信账号

