
麦肯锡预测,从2021年到2030年,电池电动汽车(BEV)的需求将增长六倍,年销量将达到约4000万辆,远高于目前的650万辆。电机、电池和电力电子设备是驱动系统中的关键组件,直接影响效率、续航里程和整体驾驶体验。更高的效率意味着电机运行过程中能量损失更少,从而延长电池寿命并提高续航里程。更高的输出功率改善了加速性能,确保电机能够应对各种驾驶条件。减少电动汽车牵引电机的振动和噪音水平对于提供平稳舒适的驾驶体验至关重要。此外,紧凑的牵引电机设计有助于最大化车内空间并减少车辆重量,从而进一步提高效率。在这种背景下,像电磁分析和设计优化这样的仿真技术,对于提升电动汽车牵引电机的性能至关重要。这些工具使工程师能够建模和分析电机内部的复杂交互,优化其设计,以实现最大效率、功率和平稳性。
电磁仿真分析和参数化设计优化的结合
将JMAG电磁分析与modeFRONTIER工作流程相结合是一种强大的仿真驱动方法,用于优化电动汽车牵引电机的设计。JMAG是一款专为电机设计而开发的综合电磁场仿真软件,提供全面的功能,如磁场、热分析和结构分析,以识别潜在的设计改进。同时,modeFRONTIER是一款过程自动化和设计优化软件,能够将JMAG的电磁分析自动化,并融入仿真工作流程中。它通过同时考虑多个性能标准,实现多目标优化。modeFRONTIER协调仿真过程,管理JMAG与其他软件之间的数据交换。工程师可以定义设计参数、目标和约束,然后利用设计探索和优化算法,系统地探索设计空间,最终达到最佳设计解决方案。
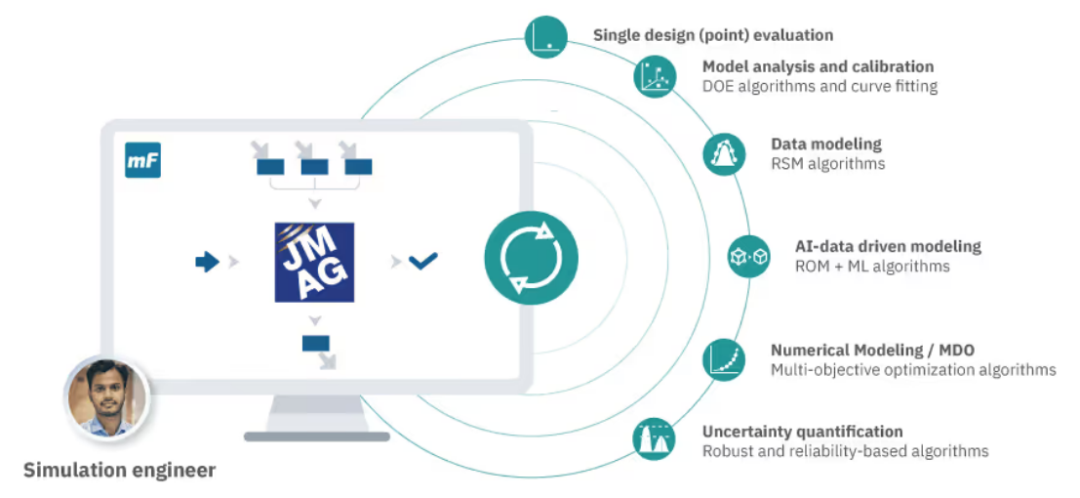
电磁仿真分析和参数化设计优化的结合
1. 设置永磁电机仿真分析并将其自动化
于modeFRONTIER工作流程中
永磁电机以其高效性、紧凑的尺寸和可靠性而闻名。在本研究中,我们旨在优化一款8极永磁电机的性能,有大量的约束条件和两种不同的工作条件:低转速[1200rpm]和高转速[9000rpm]。
该研究有11个自由参数,作为优化的输入:
· 几何参数 [Fb, L, Lm, Mw, Rs, So, Th] 定义了定子和转子的几何形状
· 两种工作条件的电流规格 [幅值, 相位]


电动牵引电机的几何形状和可变参数
永磁电机的优化需要考虑性能目标和结构限制,所有这些都作为约束条件或目标在我们的研究中进行考虑。
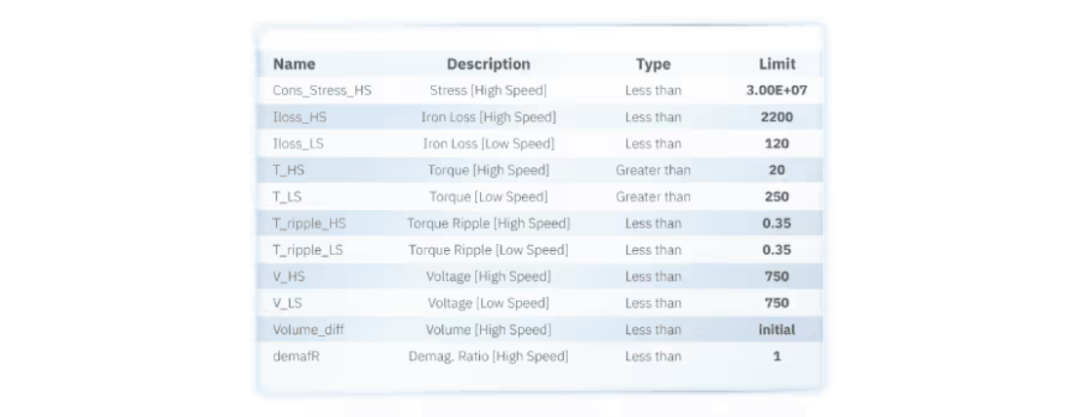
约束列表
在这个使用案例中,JMAG的牵引电机电磁分析涉及四个连续的研究步骤,每个步骤的几何形状和参数都由Analysis Group控制:
磁场分析:模拟电机内部的磁场分布,提供磁通和分布。这一分析评估电机性能,并预测会影响整体效率的损耗。
退磁分析:评估在各种操作条件下(如高温或过电流条件)永久磁铁退磁的风险。
结构分析:评估电机结构组件的机械完整性和性能。此分析考虑诸如机械应力、电机运行过程中产生的电磁力下的变形等因素。

接下来,我们将JMAG的电磁分析集成并自动化到modeFRONTIER工作流中,该工作流配置和管理输入输出变量,以及目标和约束条件,以执行设计探索和优化研究。

modeFRONTIER工作流中的设计过程自动化
2. 执行实验设计
研究首先通过实验设计(DOE)来探索设计空间,这可以使我们更好地理解优化问题的关键方面,例如变量参数化、输入/输出相关性和约束条件分析。在本研究中,我们使用均匀拉丁超立方(ULH)算法生成了300个设计。

modeFRONTIER的散点矩阵图用于DOE分析
散点矩阵图揭示了输入变量之间的低相关性,表明DOE数据集定义得很好,并且均匀地覆盖了输入参数空间。然而,300个设计中没有一个满足定义的约束条件,特别是在低速下的应力和扭矩值。这为设计优化任务提出了一个关键挑战。
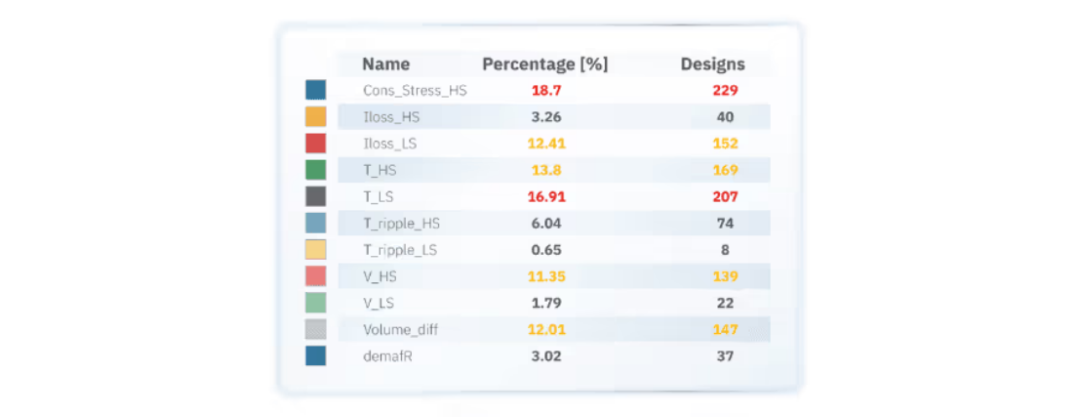
约束失效分析
优化问题的复杂性来自于变量、约束和目标的数量。为了解决这一问题,探索了使用灵敏度分析作为降低问题维度的方法。对原始参数化进行的分析显示,所有输入变量都对系统响应产生了显著影响。
3. 应用不同的设计优化技术
我们使用DOE结果作为初始种群,对多目标设计优化策略进行比较分析,以最大化扭矩(在高速和低速下)并最小化铁损(在高速下)。为了实现这一点,我们利用了modeFRONTIER的专有算法pilOPT。这种多策略自适应算法结合了局部和全局搜索方法的优点,智能地平衡了基于实际仿真和响应面(RSM)的优化,以有效地搜索帕累托前沿。

通过一步优化方法,我们已经取得了令人鼓舞的结果。该方法计算了1300个设计,找到了347个可行设计,并且获得了一个包含220个设计的Pareto前沿。
多步优化方法的目标是通过初步优化步骤识别可行区域,然后向该区域添加更多设计,最后利用所有收集到的信息初始化最终优化步骤。多步优化由以下三个步骤组成:
1. 初步优化
2. 基于主成分的设计实验(DOE)
3. 精细优化(3种不同方法)
初步优化包含了300次迭代,使用了pilOPT算法。尽管迭代次数低于第一种方法,但该算法找到了94个可行设计,足以描述可行区域。为了准确地在该区域内添加设计,我们需要一个能够表示这个复杂超空间的参数化。这就是为什么我们使用modeFRONTIER的主成分分析(PCA)工具的原因。
主成分分析(PCA)是一种统计技术,它通过保留数据的基本结构来降低数据的维度。PCA识别出数据集中最大方差的无相关方向,这些方向被称为主成分(PCs),它们捕捉了最重要的信息。这个转换使得数据集能够以更高效的方式表示,同时保留其基本特征。
PCA在高度约束优化中特别有用,原因有二:
1. 维度降低:在具有大量变量的优化问题中,PCA通过识别解释方差的最重要成分来帮助降低维度。关注这些主成分简化了优化问题,使其在计算上更容易处理。
2. 约束处理:PCA还帮助处理约束。例如,原始变量空间中的线性约束可以转换到主成分空间,从而简化其表示和操作。
在这个应用案例中,我们对输入变量进行了PCA分析,使用了第一步优化中获得的94个可行设计。虽然主成分的数量与输入变量的数量相同,但前七个主成分捕获了95.4%的方差。下图显示了按解释方差排序的主成分,每个主成分都有一个上下限,代表在主成分超空间中的可行区域。

主成分解释方差柱状图
可以通过减少变量的数量来降低问题的复杂性。这带来了两个关键的好处:
1. 降低优化问题的复杂性
2. 最小化由不重要变量引起的噪声
在这个应用案例中,我们考虑了所有的主成分(PCs),因为我们的目标是专注于重新参数化问题,而不仅仅是利用降维。通过保持相同的维度和问题复杂性,使用主成分分析(PCA)重新参数化输入变量,简化了可行超空间,从而使我们能够更有效地专注于可行区域。需要注意的是,这种方法假设94个设计足以描述可行区域。这个假设是一个关键约束,它是主观定义的。显然,我们考虑的可行设计越多,PCA分析对可行区域的表示就会越准确。两个3D散点图展示了重新参数化的有效性:左图显示,重新参数化的设计与初步步骤中的94个可行设计非常接近。相比之下,当使用原始参数化(右图)时,添加相同数量的设计并没有接近可行区域。

左:基于PCA参数化的113个DOE[ULH]
右:基于原始参数化的113个DOE[ULH]
在初步优化和通过PCA分析重新参数化之后,我们通过三种额外的方法来优化设计:
1. 原始变量和边界(Multi_1)
2. 原始变量和受限边界(Multi_2)
3. 主成分变量(Multi_3)
最大迭代次数设置为587,总共计算了1300个设计,涵盖了所有策略。
Multi_1:该方法使用原始参数化和边界。算法从713个设计开始:
· 300个来自DOE研究
· 300个来自第一次优化步骤
· 113个来自PCA重新参数化DOE
该方法找到了347个可行设计,并且得到了122个设计的Pareto前沿。
Multi_2:该方法应用原始变量,但将它们限制在第一次优化步骤中找到的可行区域边界内。优化算法从202个设计开始,这些设计经过筛选以满足这些边界条件。该方法找到了443个可行设计,并且得到了187个设计的Pareto前沿。
Multi_3:对于这种方法,modeFRONTIER工作流进行了修改,使用主成分(PCs)变量而不是原始参数化。它从207个设计开始:
· 94个来自初步步骤的可行设计
· 113个来自PCA重新参数化DOE
该方法找到了444个可行设计,并且得到了203个设计的Pareto前沿。
4. 策略比较
这项工作展示了多种方法来解决高度受限的优化问题,但并未选择某一种作为最佳方法。在最后一章,我们从不同的角度对结果进行比较,并进行了结果的稳健性分析。为了比较这四种方法的结果,我们将每种优化策略的最佳设计汇总到一个比较表中。


在目标空间中比较四种方法结果
Multi_2方法似乎提供了表现最好的设计。当我们从比较表中提取非支配设计时,发现Pareto前沿主要由Multi_2方法的设计组成。

在目标空间中显示非支配设计的3D散点图
最佳设计分布如下:

尽管Multi_3策略产生了最多的可行设计,但产生大多数最佳设计的方法是Multi_2。
5. 稳健性分析
稳健性分析旨在探索当输入参数存在不确定性时,响应如何变化。在本研究中,它提供了另一种比较所考虑的四种优化策略的方法。我们通过从每个优化策略的Pareto前沿中选择5个设计来设置分析,这些设计代表了基于共同标准定义的潜在折衷。
筛选规则:
l 低速扭矩 > 260 Nm
l 高速扭矩 > 40 Nm
对于每组五个设计,我们选择了最佳折衷方案,以最小化应力和铁损。四个输入参数被认为是随机变量:Fb、Lm、Mw、Th。
在每个选定的设计周围,采样了50个额外的设计,分布在该设计周围,使用每个变量标准差为0.05的正态分布。这导致每组总共采样了250个设计。然后,我们使用输出值的百分位数重新定义了约束函数,如下所示。
例如,给定输出的99百分位数保证了在设定的名义输入参数下,考虑到给定的不确定性,设计一旦实现,输出值将低于该百分位数的概率为99%。
然而,需要考虑两个关键限制:
1. 样本量处于进行有意义统计分析的下限,且涉及四个随机变量。因此,对于具有简单趋势的输出,我们将得到可接受的结果,但对于其他输出,结果可能不那么可靠。
2. 获取稳健解的理想方式是进行稳健优化,其中目标函数也以百分位数的形式表达,算法将基于这些重新定义的目标函数进行工作。
这些限制在我们的研究中是可以接受的,因为该用例更侧重于不同策略、方法和工具的定性比较,而不是定量分析。结果再次表明,Multi_2方法在五个选定设计中提供了最多的可行设计,表明它提供了更稳健的解。
尽管结果显示Multi_2总体上提供了最佳解,但本研究仍有一些局限性,我们不能在所有情况下明确地宣称它是最佳方法。我们获得的结果更多地侧重于方法论。我们展示了:
· 多步优化方法可以作为解决高度约束优化问题的有价值策略。
· PCA重新参数化是处理高度约束问题的强大工具,使用户能够集中精力在识别出的可行区域上。
· 稳健性分析可以用来评估获得解的稳健性,作为比较不同方法的解或从一组最佳设计中选择更稳健设计的工具。

 B站账号
B站账号

 知乎账号
知乎账号

 微信账号
微信账号